The world around us is filled with life and wonder. Upon close inspection, we find a variety of microscopic organisms moving curiously in the ocean, within the soil, etc. Our research unravels the complex dynamics within living systems by incorporating basic physical principles into mathematical modeling. This approach elucidates key mechanisms, predicts possible outcomes, and leads to exciting discoveries in mathematics and science.

We use theoretical, computational, and experimental methods in our research. The projects often start with a striking or unusual observation in the laboratory. A careful analysis of experimental data inspires a suitable set of governing equations and conditions, which are used to formulate new mathematical problems. The problems are solved by hand and computer simulations to make predictions under a broad range of conditions. The scope and validity of the predictions are tested against experimental data, and the model is refined until there is reasonable agreement with the data. This process of going back and forth between theory and experiments contributes to advances in both mathematical and scientific research.

Recent project examples

Migration of bacteria swimming through narrow passages

We observed bacteria escaping from narrow passages shortly upon entry. A stochastic model that incorporates random directional changes revealed possible mechanisms underlying bacterial migration in physically heterogeneous environments. Recent efforts are aimed at unraveling the movements of bacteria in fungal networks.

Nutrients recirculating in soil

Worms have been observed to crawl and recirculate nutrients in soil. To predict the nutrient distribution around an undulating worm, we developed a model of peristaltic pumping in a porous conduit. We are broadly interested in formulating mathematical problems associated with recirculating nutrients in soil and other porous media.

Fluid pumping near the air-water interface

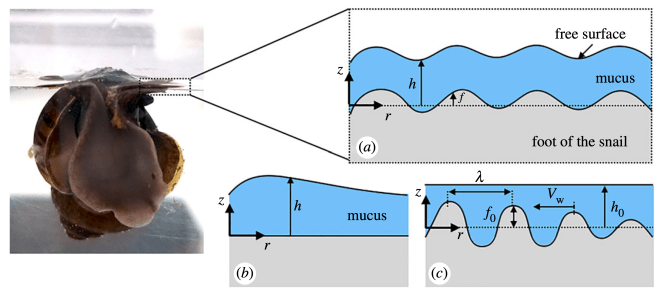We observed snails deforming their foot into a funnel-like structure and producing a large-scale current around the body while feeding on the water surface. Inspired by this behavior, we formulated a model using partial differential equations to predict the amount of fluid pumped by a deformable wavy surface. A related project modeled the dynamics of small ripples, which are potentially used by surface-dwelling insects for sensing and communication on the water surface.

Flow-based sensing of suspended bodies

Blind cavefish and zooplankton show highly unsteady movements while feeding in water. We formulated mathematical inverse problems to study how distant food particles could be detected and located from a distance based on flow sensing. A related project examined how a planktonic copepod evades an  approaching predatory fish by relying on hydrodynamic cues.

Previous project examples

Emergent behavior of synthetic microswimmers

Experiments with chemically active microparticles revealed the emergence of life-like behaviors, such as brief trapping around spherical obstacles and migration against gravity. These phenomena were modeled by incorporating asymmetry in fluid slip on the particle’s surface.

Locomotion of planktonic copepods

Copepods swim and maneuver efficiently in viscous fluids by coordinating their appendages in a metachronal pattern. We developed simplified models of multi-legged swimmers, explored optimal gaits using geometric control theory, and tested the models using scaled up robots in the laboratory.